Easy DSP with Vult
Functions with memory simplify writing Digital Signal Processing (DSP) code since a mem variable can be used to as a single sample delay z^1. I order to implement the Digital Biquad Filter (direct form 2) we can take the equations directly from Wikipedia: https://en.wikipedia.org/wiki/Digital_biquad_filter.
We can see the architecture and the equations here:


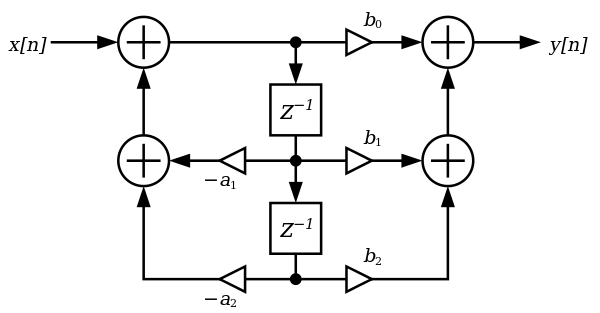
We can implement these equations in Vult as follows.
The variables w1 and w2 represent the terms w[n-1] and w[n-2]. The variables y0 and x0 represent y[n] and x[n]. The coefficients of the filter are b0, b1, b2, a0 and a2 which are calculated depending on the filter. We can see that w1 and w2 are declared as mem variables since we want them to keep their value every time the function is called.
Now that we have the architecture of the biquad, we can design filters. In order to design a filter we need to calculate the coefficients. Here we are gonna follow the formulae show in the Audio-EQ-Cookbook. The code for the filter is the following:
In the code, x is the input signal w0 is the cut frequency (in radians) and q controls the resonance. This filter is variable and we can adjust the cut frequency and the resonance. In order to achieve that we need to calculate the coefficients every time the cut or resonance changes. We can see in the above code that the implementation is not very efficient since it calculates the coefficients every sample. To improve it can use the function change that we defined in the Functions with Memory tutorial.
fun lowpass(x,w0,q) { mem b0,b1,b2,a1,a2; if(change(w0) || change(q)) { val cos_w = cos(w0); val alpha = sin(w0)/(2.0q); val den = 1.0 + alpha; a1 = (-2.0cos_w)/den; a2 = (1.0 - alpha)/den; b0 = ((1.0 - cos_w)/(2.0den)); b1 = (1.0 - cos_w)/den; b2 = ((1.0 - cos_w)/(2.0den)); } return biquad(x,b0,b1,b2,a1,a2); }
In the example above, we have changed the declaration of the coefficients to mem variables because we want to remember the previous values. By wrapping the calculation inside the if-statement we recalculate the coefficients every time the values of fc and q change.
Now that we have the filter, we can use it as part of a bigger program. For example:
… // some other here
val s_1 = …; // generate a signal val s_2 = …; // generate a signal
// the first filter is controlled by control_1 and control_2 val s_1_filtered = lowpass(s_1, control_1, control_2);
// the second filter is controlled by control_3 and control_4 val s_2_filtered = lowpass(s_2, control_3, control_4);
return s_1_filtered + s_2_filtered; }
Just for you to remember, every time you call the function lowpass and independent memory space is generated. Therefore, the filter for signal s_1 and s_2 do not interfere each other.
In the next tutorial we are gonna create a state-variable filter and we are gonna show how easy is to do oversampling in Vult.